Evaluating Object Detection Models

Object detection is one of the most fundamental tasks in computer vision. The goal of a detection model is to place bounding boxes correctly around objects of predefined classes in an image. A detection is consisted of three components: a bounding box, a class label and a confidence score. The class label often belongs to a set of predefined object categories, and the confidence score is the probability of the bounding box belonged to that class. Examples of detection results are visualized below.

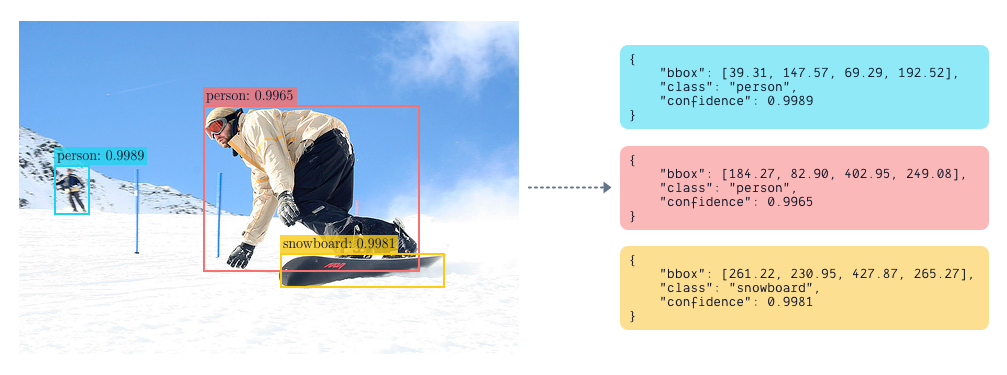
As the field has been studied extensively over the past several decades, the research community seems to have agreed on several standard evaluation metrics. The detection evaluation metrics quantify the performance of the detection algorithms/models. They measure how close the detected bounding boxes are to the ground-truth bounding boxes.

Bounding box format

The bounding box is a rectangle covering the area of an object. I mean, it sounds pretty trivial, doesn't it? However, there is no consensus of a standard format of what a bounding box is represented in practice. In fact, each dataset defines their own format of bounding boxes. There are at least three popular format:

• The Pascal VOC dataset presents each bounding box with its top-left and bottom-right pixel coordinates.
• In the COCO dataset, each bounding box is in the format of $[x, y, w, h]$ where $[x, y]$ is the top-left pixel coordinate, and $w$ and $h$ are the absolute width and height of the box, respectively.
• Other datasets, such as Open Image, defines the format of their bounding boxes as $[x_c, y_c, w_{\mathrm{rel}}, h_{\mathrm{rel}}]$, where $[x_c, y_c]$ is the normalized coordinates of the center of the box, and $w_{\mathrm{rel}}$ and $h_{\mathrm{rel}}$ are the relative width and height of box, normalized by the width and height of the image respectively.

These nuances often create confusions and require extra attention when working with different datatsets, as well as interpreting the detection results of the models on the corresponding dataset.

Intersection over Union

Let's ignore the confidence score for a moment, a perfect detection is the one whose predicted bounding box has the area and location exactly same as the ground-truth bounding box. Intersection over Union (IoU) is the measure to characterize these two conditions of a predicted bounding box. It is the base metric for most of the evaluation metrics for object detection.

As its name indicates, IoU is the ratio between the area of intersection and the area of union between a predicted box $\hat{b}$ and a ground-truth box $b$, as illustrated in the figure below

IoU is stemmed from the Jaccard Index, a coefficient measure the similarity between two finite sample sets.

IoU varies between $0$ and $1$. An $\mathrm{IoU} = 1$ means a perfect match between prediction and ground-truth, while $\mathrm{IoU} = 0$ means the predicted and the ground-truth boxes do not overlap. By varying the threshold $\mathrm{IoU} = \epsilon$ we can control how restrictive or relaxing the metric is. Moreover, this threshold is used to decide if a detection is correct or not. A correct, or positive, detection has $\mathrm{IoU} \geq \epsilon$, otherwise, the detection is an incorrect, or negative one. More formally, predictions are classified as True Positive (TP), False Positive (FP) and False Negative (FN)

• True positive (TP): A correct detection of the ground-truth bounding box;
• False positive (FP): An incorrect detection of a non-existing object or a misplaced detection of an existing object;
• False negative (FN): An undetected ground-truth bounding box.

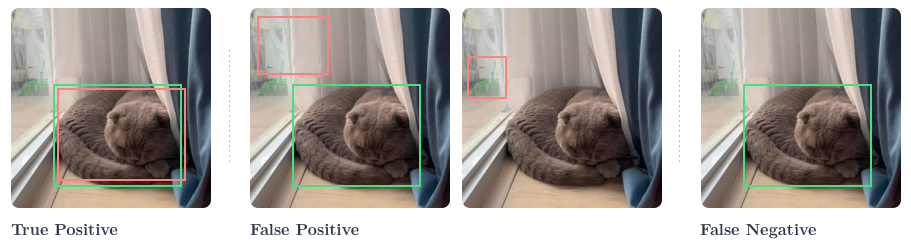
In the leftmost illustration of a TP example, there is a ground-truth box of the cat in the image and there is a prediction that is close enough to the ground-truth. In FP examples, either the predicted box is too off w.r.t to the ground-truth, or there is prediction of an object that has no corresponding ground-truth box in the image. Lastly, in the FN example, the object is there with a ground-truth box, but there is no prediction for it.

Precision and Recall

Precision reflects how well a model is in predicting bounding boxes that match ground-truth boxes, i.e. making positive predictions. It is the ratio between number of TP(s) to total number of positive predictions.

For example, if a model makes 100 bounding-box predictions for the cats in the dataset, and 90 of them are correct predictions (i.e., each box has an IoU higher than predefined threshold, say $\epsilon = 0.5$, w.r.t to its corresponding ground-truth), then the precision of the model for the cat label is 90 percent. Precision is often expressed as percentage, or within the range of $0$ to $1$.

A low precision indicates that the model makes a lot of FP predictions. In contrast, a high precision is when the model either making lots of TP, or very few FP predictions.

Recall is the ratio between the number of TP and the actual number of relevant objects.

Recall reflects the sensitivity of the model in detecting ground-truth objects. Similar to precision, recall can also be expressed as percentange, or value between $0$ and $1$.

Interpretations of Precision-Recall

• A high precision and low recall implies most predicted boxes are correct, but most of the ground-truth objects have been missed.
• A low precision and high recall implies that most of the ground-truth objects have been detected, but the majority of the predictions that the model make is incorrect.
• A high precision and high recall tells us that most ground-truths have been detected and the detections are good — a desire property of an ideal detector.

Average Precision

So far we haven't touched the confidence score when discussing the precision and recall. But it can be taken into account for those metrics by considering the predictions whose confidence scores are higher than a threshold $\tau$ positives, otherwise, negatives.

We can see that $\mathrm{TP}(\tau)$ and $\mathrm{FP}(\tau)$ are decreasing functions of $\tau$, as $\tau$ increases, less detections will be regarded as positives. On the other hand, $\mathrm{FN}(\tau)$ is an increasing function of $\tau$. Moreoever, the sum $\mathrm{TP}(\tau) + \mathrm{FN}(\tau)$ is a constant, independent of $\tau$, as it equals to all the ground-truths. Therefore, the recall $\mathrm{Rc}$ is a decreasing function of $\tau$, while we can't really say anything about the monotonicity of the $\mathrm{Pr}$. As a result, if we plot the precision-recall curve, it often has a zigzag-like shape.

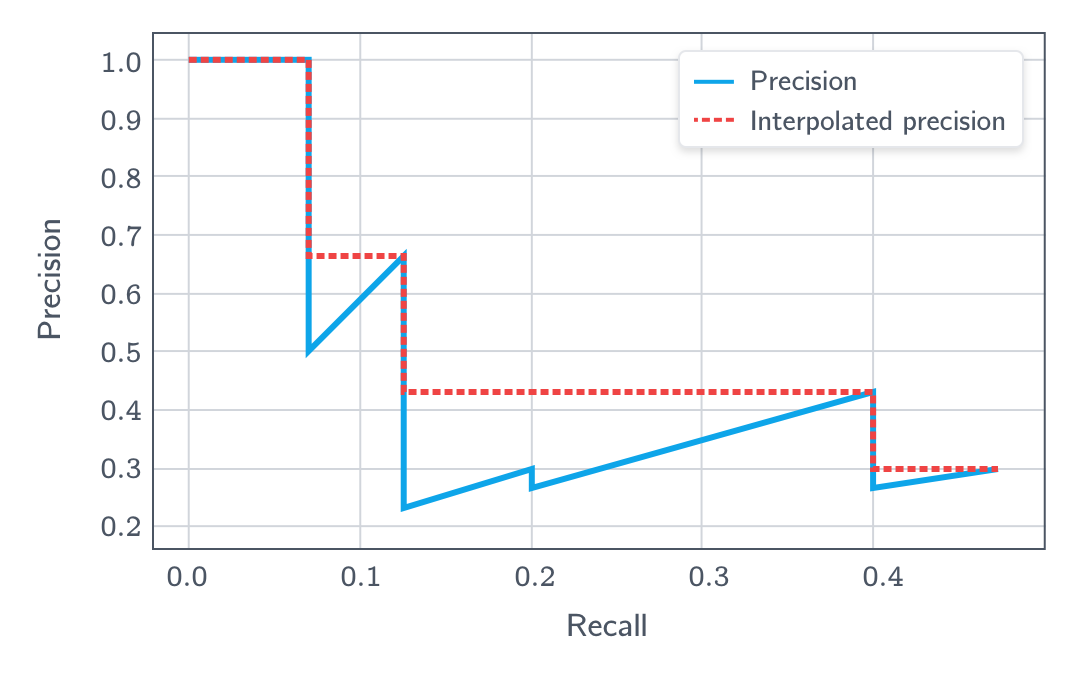
The average precision is the area under the precision-recall curve, and is formally defined as

In practice, the precision-recall is often of zigzag-like shape, making it challenging to evaluate this integral. To circumvent this issue, the precision-recall curve is often first smoothed using either 11-point interpolation or all-point interpolation.

11-point interpolation

In this method, the precision-recall curve is summarized by averaging the maximum precision values at a set of 11 equally spaced recal levels $[0, 0.1, 0.2, \dots, 1]$ , as given by

where $P_{\mathrm{interp}} (R)$ is the interpolated precision at recall $R$, and is defined asWhat it means is that instead of using the $P(R)$ at every observed recall level, the AP is obtained by considering the maximum precision $P_{\mathrm{interp}} (R)$ whose recall value is greater than $R$.

All-point interpolation

In this approach, instead of taking only serveral points into consideration, the AP is computed by interpolating at each recall level, taking the maximum precision whose recall value is greater than or equal to $R_{n+1}$.

where

mean Average Precision - mAP

The AP is often computed separately for each object class; then, the final performance of a detection model is often reported by taking the average over all classes, or, to obtain the mean average precision - mAP.

where $\mathrm{AP}_i$ is the average precision for the $i$th class.

Object detection challenges and their APs

Object detection is a very active field of research, especially with the flourishment of deep learning methods, it has been a challenge to find an unified approach to compare the performance of detection models. Indeed, each dataset and object detection challeges often use slightly different metrics to measure the detection performance. The table below lists some popular benchmark dataset and their AP variants.

The COCO detection challenge introduces more fine-grained AP metrics w.r.t. object sizes. The main motivation is that object size significantly affects the detection performance; thus, it is also informative to report AP metrics for different object scales.

• $\mathrm{AP}_S$: AP for small objects, i.e., area $< 32^2$ pixels
• $\mathrm{AP}_M$: AP for medium objects, i.e., $32^2 <$ area $< 96^2$ pixels
• $\mathrm{AP}_L$: AP for large objects, i.e., area $> 96^2$ pixels